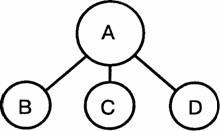
 , где А — делимое
понятие, В, С,
D — члены деления.
, где А — делимое
понятие, В, С,
D — члены деления.Билет № 20
1. Логическая операция деления понятия. Выди деления. Деление по видоизменению признака. Правила деления понятий.
Логическая
операция, раскрывающая объем понятия, называется делением.
В операции деления следует различать делимое понятие — объем которого
следует раскрыть, члены деления — соподчиненные виды, на которые делится
понятие (они представляют собой результат деления), и основание деления —
признак, по которому производится деление. Логическая операция деления может
быть представлена схемой  , где А — делимое
понятие, В, С,
D — члены деления.
, где А — делимое
понятие, В, С,
D — члены деления.
Виды деления. Различают деление 1) по видоизменению признака и 2) дихотомическое деление. 1. Деление по видоизменению признака. Основанием деления является признак, при изменении которого образуются видовые понятия, входящие в объем делимого (родового) понятия. Например, государства в зависимости от формы государственного устройства делятся на унитарные и федеративные; право по форме своего выражения — на правовой обычай, юридический прецедент и нормативный акт. Оъективность основания. Правила деления. В процессе деления понятия необходимо соблюдать четыре правила, которые обеспечивают четкость и полноту деления. 1. Деление должно быть соразмерным. Нарушения правила –неполное деление и деление с лишними членами.
2. Деление должно производиться только по одному основанию.
3. Члены деления должны исключать друг друга.
4. Деление должно быть непрерывным Ошибка в делении называется скачком в делении.
Дихотомическое деление представляет собой деление
объема делимого понятия на два противоречащих понятия. Если А— делимое понятие,
то членами деления будут два понятия: В и не-В. Дихотомическое
деление не всегда заканчивается установлением двух противоречащих понятий.
Иногда отрицательное понятие вновь делится на два понятия, что помогает выделить
из большого круга предметов группу предметов, интересующих нас в каком-либо
отношении. Классификация. Особым видом деления является классификация,
представляющая собой распределение предметов по группам (классам), при
котором каждый класс имеет свое постоянное, определенное место. Целью
классификации является систематизация знаний, поэтому от деления она отличается
относительно устойчивым характером и сохраняется более или менее длительное
время. Кроме того, классификация образует развернутую систему, где каждый член
деления вновь делится на новые члены, разветвляясь на множество классов.
2. Научная индукция: метод сопутствующих изменений. Метод применяется при
анализе случаев, в которых имеет место видоизменение одного из предшествующих
обстоятельств, сопровождаемое видоизменением исследуемого действия.
Предыдущие индуктивные методы основывались на повторяемости либо отсутствии
определенного обстоятельства. Однако не все причинно связанные явления допускают
нейтрализацию или замену отдельных составляющих их факторов. Например, исследуя
влияние трения на скорость движения тела, невозможно в принципе исключить само
трение. Точно так же определяя влияние Луны на величину морских приливов,
невозможно изменить массу Луны. Единственным способом обнаружения причинных
связей в таких условиях является фиксация в процессе наблюдения
сопутствующих изменений в предшествующих и последующих явлениях. Причиной
в этом случае выступает такое предшествующее обстоятельство, интенсивность или
степень изменения которого совпадает с изменением исследуемого действия. Если
обозначить символами А, В, С предшествующие обстоятельства, каждое из
которых не может быть опущено или заменено; индексами 1,2,...,
n — степень
изменения этих обстоятельств; символом
d — интересующее нас действие, то
рассуждение по методу сопутствующих изменений принимает следующий вид: 1)
АВС1 вызывает d1 2) АВС2 вызывает d2
n) АВСn
вызывает dn
По-видимому, С является причиной d. Применение метода сопутствующих изменений
также предполагает соблюдение ряда условий. (1) Необходимо знание о всех
возможных причинах исследуемого явления. Такими обстоятельствами выступают А, В
и С: AvBvC.
(2) Из приведенных обстоятельств должны быть элиминированы те, которые не
удовлетворяют свойству однозначности причинной связи. Так, во всех трех случаях
А и В не могут быть причиной d, ибо с изменением d и первое, и второе остаются
неизменными. А и В элиминируются, ибо неизменяющееся не может быть причиной
изменяющегося, что косвенно указывает на С как на единственную среди возможных
причин. (3) Среди предшествующих выделяют единственное обстоятельство,
изменение которого сопутствует изменению действия. В приведенной схеме
такую роль выполняет С, изменение интенсивности которого от С1 до Сn
сопровождается изменением интенсивности
d — от d1 до dn.
Сопутствующие изменения могут быть прямыми и обратными. Прямая
зависимость означает: чем интенсивнее проявление предшествующего фактора,
тем активнее проявляет себя и исследуемое явление, и наоборот, — с падением
интенсивности соответственно снижается и активность или степень проявления
действия. Обратная зависимость выражается в том, что интенсивное
проявление предшествующего обстоятельства замедляет активность или уменьшает
степень изменения исследуемого явления. Схема рассуждения имеет следующий
вид: AvBvC,lA,lB
По-видимому, С. Во внимание принимаются не
любые, а лишь пропорционально нарастающие либо убывающие измененияРассуждения
по методу сопутствующих изменений применяются при выявлении не только причинных,
но и других, например функциональных связей, когда устанавливают
зависимость между количественными характеристиками двух явлений. В этом случае
важное значение приобретает учет характерной для каждого рода явлений
шкалы интенсивности изменений, в рамках которой количественные
изменения не меняют качества явления. В любом случае количественные изменения
имеют нижнюю и верхнюю границы, которые называются пределами
интенсивности. Любой процесс количественных изменений имеет свои
критические точки, которые следует учитывать при применении метода
сопутствующих изменений, эффективно действующего лишь в рамках шкалы
интенсивности. Использование метода без учета пограничных зон количественных
изменений может приводить к логически некорректным результатам.
Классификация. Особым видом деления является классификация,
представляющая собой распределение предметов по группам (классам), при
котором каждый класс имеет свое постоянное, определенное место. Целью
классификации является систематизация знаний, поэтому от деления она отличается
относительно устойчивым характером и сохраняется более или менее длительное
время. Кроме того, классификация образует развернутую систему, где каждый член
деления вновь делится на новые члены, разветвляясь на множество классов.
2. Научная индукция: метод сопутствующих изменений. Метод применяется при
анализе случаев, в которых имеет место видоизменение одного из предшествующих
обстоятельств, сопровождаемое видоизменением исследуемого действия.
Предыдущие индуктивные методы основывались на повторяемости либо отсутствии
определенного обстоятельства. Однако не все причинно связанные явления допускают
нейтрализацию или замену отдельных составляющих их факторов. Например, исследуя
влияние трения на скорость движения тела, невозможно в принципе исключить само
трение. Точно так же определяя влияние Луны на величину морских приливов,
невозможно изменить массу Луны. Единственным способом обнаружения причинных
связей в таких условиях является фиксация в процессе наблюдения
сопутствующих изменений в предшествующих и последующих явлениях. Причиной
в этом случае выступает такое предшествующее обстоятельство, интенсивность или
степень изменения которого совпадает с изменением исследуемого действия. Если
обозначить символами А, В, С предшествующие обстоятельства, каждое из
которых не может быть опущено или заменено; индексами 1,2,...,
n — степень
изменения этих обстоятельств; символом
d — интересующее нас действие, то
рассуждение по методу сопутствующих изменений принимает следующий вид: 1)
АВС1 вызывает d1 2) АВС2 вызывает d2
n) АВСn
вызывает dn
По-видимому, С является причиной d. Применение метода сопутствующих изменений
также предполагает соблюдение ряда условий. (1) Необходимо знание о всех
возможных причинах исследуемого явления. Такими обстоятельствами выступают А, В
и С: AvBvC.
(2) Из приведенных обстоятельств должны быть элиминированы те, которые не
удовлетворяют свойству однозначности причинной связи. Так, во всех трех случаях
А и В не могут быть причиной d, ибо с изменением d и первое, и второе остаются
неизменными. А и В элиминируются, ибо неизменяющееся не может быть причиной
изменяющегося, что косвенно указывает на С как на единственную среди возможных
причин. (3) Среди предшествующих выделяют единственное обстоятельство,
изменение которого сопутствует изменению действия. В приведенной схеме
такую роль выполняет С, изменение интенсивности которого от С1 до Сn
сопровождается изменением интенсивности
d — от d1 до dn.
Сопутствующие изменения могут быть прямыми и обратными. Прямая
зависимость означает: чем интенсивнее проявление предшествующего фактора,
тем активнее проявляет себя и исследуемое явление, и наоборот, — с падением
интенсивности соответственно снижается и активность или степень проявления
действия. Обратная зависимость выражается в том, что интенсивное
проявление предшествующего обстоятельства замедляет активность или уменьшает
степень изменения исследуемого явления. Схема рассуждения имеет следующий
вид: AvBvC,lA,lB
По-видимому, С. Во внимание принимаются не
любые, а лишь пропорционально нарастающие либо убывающие измененияРассуждения
по методу сопутствующих изменений применяются при выявлении не только причинных,
но и других, например функциональных связей, когда устанавливают
зависимость между количественными характеристиками двух явлений. В этом случае
важное значение приобретает учет характерной для каждого рода явлений
шкалы интенсивности изменений, в рамках которой количественные
изменения не меняют качества явления. В любом случае количественные изменения
имеют нижнюю и верхнюю границы, которые называются пределами
интенсивности. Любой процесс количественных изменений имеет свои
критические точки, которые следует учитывать при применении метода
сопутствующих изменений, эффективно действующего лишь в рамках шкалы
интенсивности. Использование метода без учета пограничных зон количественных
изменений может приводить к логически некорректным результатам.